DRO论文阅读笔记
Published:
一种保护LLM防御有害查询的方法是预先设置的模型输入带有人工合成的安全提示(safety prompt),通常包含对模型行为的明确指导和界限,但这种方式的工作机制没有很明确的研究,本文做了两种假设:(1) 模型不能很好地区分有害查询和无害查询,而安全提示增强了模型的有害识别能力。(2) 模型可以识别有害查询,但不能拒绝有害查询,而安全提示增加了整体拒绝(即拒绝提供帮助)的概率。然后通过可视化分析对机制进行了研究,最终提出了一种新的prompt表征优化方法。
Safety Prompt是如何工作的
为了理解safety prompt是如何工作的,本文首先做了一个实验。本文准备了一个有害和无害问题的数据集,然后将这个数据集中的查询发给LLM,包括添加不同的safety prompt的查询版本,最后使用最后一个input token的最后一个模型层的隐层表示进行分析。这个token之后LLM应当获取了查询的所有知识,然后要开始生成对应的回答了。这种隐藏状态也被一个语言建模头(线性映射)投射到下一个标记预测中,暗示了相应表示空间中的线性结构,从而支持进行PCA降维,降维结果如图所示。
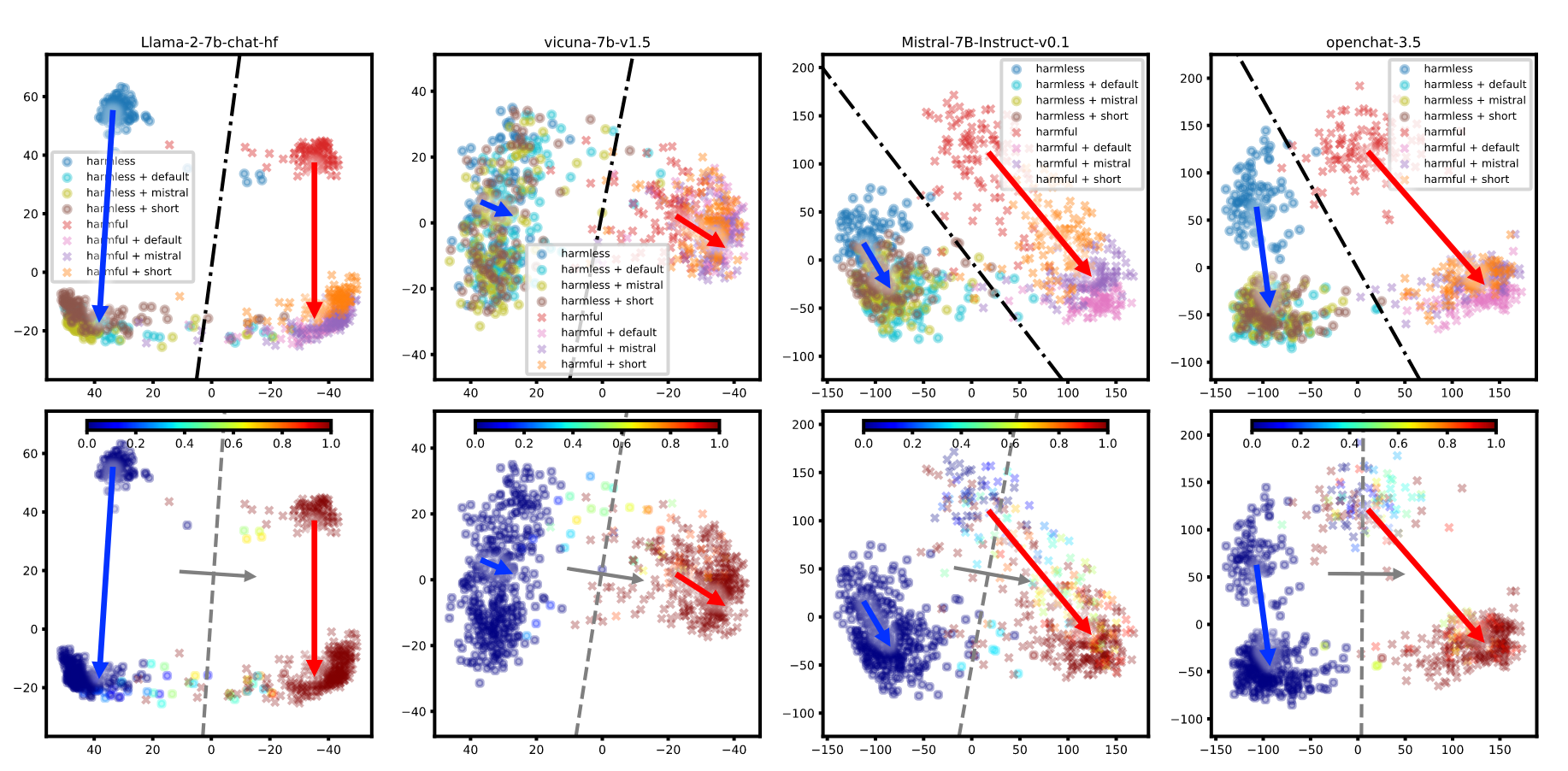
可视化结果说明在没有安全提示的情况下,有害查询和无害查询可以在很大程度上被区分,其边界(黑色链点状线条)可以很容易地通过逻辑回归以查询的危害性为标签进行拟合。添加safety prompt并没有很明显地提升可区分度。说明第一种假设可能是错的,安全提示并不能增强模型有害识别能力。
但另一方面,不同的safety prompt在将查询的表示向相似的方向移动,运动方向通常沿着”拒绝方向”具有非零分量,在该方向上拒绝概率增加,这点在有害的查询上尤其明显。这些运动也增加了对无害查询的拒绝概率,并导致错误拒绝的增加。安全提示使查询的表示朝着”高拒绝”的方向移动,从而增加模型的整体拒绝概率。
safety prompt 优化方法
提示驱动的安全保障方法有其不足,即人为设计的safety prompt的有效性随提示和模型的不同而存在较大差异。根据前面的观察结果,本文提出了一种方法来自动优化连续安全提示,命名为DRO,代表Directly Representation Optimizaiton。其核心思想是根据查询的有害程度,使查询的表示沿着或相反于拒绝方向移动。
DRO首先锚定一个模型的低维表示空间,该空间捕获与查询危害性和安全提示影响相关的特征,这些特征与模型的拒绝行为相关。然后估计指示模型的拒绝概率增加的拒绝方向。将最后一个input token的表征表示为\(x\in \mathbb{R}^n\),向低维空间的映射由使用锚点数据计算的前m个主元给出。
\[g:\mathbb{R}^n\rightarrow\mathbb{R}^m,g(x)=V^T(x-a)\]其中\(V\in\mathbb{R}^{n\times m}(n<<m)\)和\(a\in\mathbb{R}^n\)分别表示m个主成分和中心化向量。然后使用锚点数据的经验拒绝概率来拟合逻辑回归。
\[f_r(x):\mathbb{R}^m\rightarrow\mathbb{R},f_r(x)=w_r g(x)+b_r\]法向量\(w_r\)表示拒绝概率增加的估计拒绝方向。锚点数据不做修改,仅用于学习上述逻辑回归的参数。
然后,DRO通过将安全提示视为连续的、可训练的嵌入来优化安全提示。使用\(x_{\theta}\)表示前置了连续安全提示\(\theta\)所对应的查询的隐层状态,\(x_0\)表示前置了初始的安全提示\(\theta_0\)的查询的隐层状态。DRO使用二值交叉熵作为优化目标
\[\mathcal{L}_r(\theta)=-l\log\sigma(f_r(x_{\theta})-f_r(x_0))-(1-l)\log(1-\sigma(f_r(x_{\theta})-f_r(x_0)))\]\(l\in\{0,1\}\)代表问题的有害性。目标函数会给有害的查询更高的拒绝概率,而给无害的查询更低的拒绝概率。
相似的,本文还计算了一个有害性识别损失\(\mathcal{L}_h(\theta)\),计算方式基本一致,只是最后以查询的有害性为目标。有助于保持识别有害无害查询的能力。
最后DRO添加了一个正则项,用于处理直接优化带来的原始表象的退化问题。具体来说,当监督信号仅作用于\(x\)的\(m\)维特征时,其余\(n-m\)维特征的信息会丢失,从而影响生成质量。在降维函数\(g\)中,变换矩阵\(V\)包含\(m\)个单位长度的正交向量。我们可以将\(V\)化成一个正交矩阵\(Q=[V; U]\in\mathbb{R}^{n\times n}\),其中\(U\in\mathbb{R}^{n\times(n-m)}\)是任意的,可以通过Gram-Schmidt算法很容易地得到。\(Q\)保持向量长度(在欧几里得范数下)的性质可以得到
\[\lVert(x_{\theta}-x_0)\rVert^2=\lVert Q^T(x_{\theta}-x_0)\rVert^2 \\ = \lVert V^T(x_{\theta}-x_0)\rVert^2+\lVert U^T(x_{\theta}-x_0)\rVert^2 \\ =\lVert g(x_{\theta})-g(x_0)\rVert^2+\lVert U^T(x_{\theta}-x_0)\rVert^2\]LHS项为新隐状态\(x\)与初始隐状态\(x_0\)之间的变化量。第一个RHS项是提取的与安全提示和查询有害性相关的m维特征的差异,通过上面的损失函数将其放大。第二个RHS项表示剩余\(n-m\)维的信息变化,它独立于前面提取的\(m\)个特征。因此,为了将\(\lVert xθ-x0\rVert\)限制在合理的变化范围内,我们可以使用第二个RHS项进行正则化
\[\mathcal{L}_U(\theta)=\lVert U^T(x_{\theta}-x_0)\rVert^2/n\]最后将三个损失联合训练,对safety prompt进行优化。